A granny summary of an article by Dror Dotan and Nadin Brutman
Syntactic chunking reveals a core syntactic representation of multi-digit numbers, which is generative and automatic
“You don’t have to be a mathematician to have a feel for numbers.”
— John Nash
Throughout the history, many great philosophers have asked what numbers are. Pythagoras and his followers, for example, thought that numbers are the key to explaining the secrets of the universe (an idea that was borrowed into Douglas Adams’ “The Hitchhiker’s Guide to the Galaxy”). They also thought that numbers are no less real than any other object in our world. More than two millennia later, Emmanuel Kant claimed quite the opposite: that mathematical truths do not originate in the world itself, but are a-priori perceptions through we humans interpret our experience of the world. At the turn of the 21st century, we address the question “what are numbers?” not only philosophically but also from a cognitive perspective, and we ask a question that in a way echoes Kant’s view: How does our brain understand numbers?
In the last few decades, the common view is that humans perceive numbers in at least 3 ways, using 3 different cognitive mechanisms. We have a mechanism that handles number words (“three”); a mechanism that handles digits (“3”); and a mechanism that handles non-symbolic quantities (“”) and gives us an intuitive feeling of roughly how many objects I have here. This division into 3 mechanisms is known as the triple-code model.
Chances are that you are now thinking to yourself – wait a second, something is missing! Where is the part in which we actually understand the number itself? Well, it may sound strange, but the triple-code model does not describe any such part. In fact, the model pretty much assumes that there is no “core understanding of the number itself”. There are 3 cognitive representations of the numbers and that’s all. The combination of these 3 representations is what gives us the feeling that we understand the number.
The triple-code model is well supported by quite a few studies. At present, this is the predominant cognitive model of how humans process numbers. Indeed, the story of 3 representations seems to hold very well when we consider relatively small numbers (single-digit numbers and even beyond). However, when we get to larger numbers, things get more complicated – perhaps not surprisingly, because the triple-code model seems more interested in the multiple representations, and less interested in large multi-digit numbers.
For example, consider the number 42. The triple-code model will correctly emphasize that we can represent it as digits (42), as words (forty-two), and as quantity (OK I won’t write 42 dots here, so you’ll have to imagine). But there’s another issue here – one that is not contradicted but also not explained by the triple-code model: we know that 42 is 4 decades and 2 units. In short, we understand the decimal structure of numbers.
Where and how does this happen – the understanding of the decimal structure?
The decimal system is an ingenious system. Multi-digit numbers may seem natural to us, but it took mankind a very long time to come up with the idea of a place-value system – i.e., that the same digit, when appearing in different positions in the number, represents different values and is often said as different words. By the way, the first to have come up with this idea were probably the Babylonians, although they didn’t use base-10 numbers but base-60. Moreover, the complexity of the decimal system is evident not only from history. Even at the 21st century, if you think that multi-digit numbers are “natural”, think again. For example, even after children learn the first 10 digits, it takes them many more years to understand the place-value principle and to be able to use multi-digit numbers properly. And there are quite a lot of educated adults – our estimate is about 10% of the population – who have a serious difficulty dealing with multi-digit numbers.
To get a feeling of the difficulty involved in coping with multi-digit numbers, think of the number 804,720,321,600. How do you say it? What is the quantity it represents?
The answer is that you say “Eight hundred and four billion, seven hundred and twenty million, three hundred twenty-one thousand and six hundred” (by the way, this is not the only way to say it – there is more than one system for the names of very large numbers). I am guessing that many of you knew this, but also that it took you a second to come up with the number’s verbal form, and that the number name didn’t just pop straight into your mind like 42 did. You probably used some strategy, e.g., counting the number of digits. As for the quantity represented by this number – you probably know it’s a lot, you may have even thought that it’s about 1012, but it’s still probably very hard for you to grasp intuitively how much this actually is.
So what’s the story with multi-digit numbers? Do we really understand them intuitively, like we understand the number 3? Or perhaps we don’t really understand them, and we merely have a set of rules and strategies that enable us to use these numbers?
The key point is what we call the syntactic structure of numbers – this aspect of the number that reflects its decimal structure. Our ability to get that 42 has a decade digit (4) and a unit digit (2), and similarity to get that the long number above contains 12 digits, and to get the decimal role of each digit (and also some other bits of information… but we don’t get into it now).
So now I’d like to tell you about a study of ours, which aimed to examine precisely this: do people understand the syntactic structure of numbers. We were specifically interested to know whether humans not only the get low-level syntactic properties of the number (e.g. how many digits it has), but also have an intuitive understanding – a cognitive representation – of the number’s full syntactic structure.
To answer this question, we used a neat method, based on a simple memory task. The participants in our experiment heard a sequence of number words and then repeated it. The trick was that some sequences were grammatical, i.e., the series of words formed a valid number name (e.g., “three hundred twenty one”), whereas other sequences contained precisely the same words but in a different order, such that the sequence was not grammatical (“one three twenty hundred”). The idea was simple: if the participants remember each number as merely a series of words, i.e., they do not represent the number’s syntactic structure, they shouldn’t care about the order of words, so grammaticality wouldn’t make any difference. In both examples above, the sequence contains 4 words, so the memory challenge – and consequently the participant’s accuracy – should be identical in both sequences. If, on the other hand, the participants do represent the number’s syntactic structure, then for them the two sequences are dramatically different from each other. They will still perceive the non-grammatical sequence as a series of independent words, but they would be able to perceive the grammatical sequence as a single unit, a multi-digit number, rather than as a series of words. Cognitive researchers of memory call this phenomenon chunking, because the participants “pack” several words into a single chunk in memory; and there are zillions of studies showing that chunking improves the performance in memory tasks, including in repetition tasks like ours. In short, if the participants represent the numbers’ syntactic structure, they should remember the grammatical sequences better than the non-grammatical ones. And this was precisely the case:
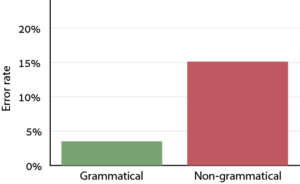
Figure 1: The error rate was lower when repeating grammatical sequences (green) than when repeating non-grammatical ones (red).
I bet that you could guess the results even before you read what they were: you could probably feel for yourself that remembering the grammatical sequence was easier than remembering the non-grammatical one. The reason you could feel it is that this effect, which we call “syntactic chunking”, is not negligible – it’s really quite strong. This may convince us intuitively that the cognitive representation of number syntax is indeed significant.
What did we learn from this study? We learned that when people think of numbers, they don’t get just the digits and words, but also the number’s syntactic-decimal structure. Critically, this syntactic-decimal structure is not merely something we know at the theory-of-math level, because we learned it at school; we know it intuitively, because we have a cognitive representation of this structure, and our brain has automatic processes that extract relevant information from the number (e.g., how many digits it has) and uses this information to create the syntactic representation.
What does this syntactic representation look like, how do we create it, and what are the implications of all this to education – i.e., to how we should teach numbers in school? Our study provided a few answers to these questions, but also left many open questions. If you’re interested in these details, you’re welcome to read the article.
